新しい結晶法と具体的テーマ

ニオブ酸リチウム融液のイオン性に起因する結晶化起電力

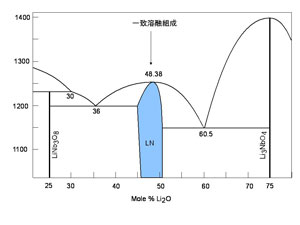
図1：Li2O­Nb2O5 状態図	本研究の概要 通常、状態図における一致溶融組成（コングルエント組成）では、融液中の溶質組成と固相中の溶質組成が等しく、 各溶質の平衡分配係数は１であると考えられている。しかしながら、酸化物結晶の融液中にはイオン種が存在し [1]、そのイオン種が独自の分配係数を持つために、一致溶融組成であっても、イオン種を含めたすべての溶質の 平衡分配係数が必ずしも１とならない[2,3]。酸化物融液がイオン性を 示すことは以前から知られていたが、これまで結晶成長におけるイオンの分配やそれに起因する結晶化起電力 [4]についてはほとんど無視されてきている。 本研究[5]では、マイクロ引き下げ法を用いた界面近傍の内部電場測定 及びその解析を通して、以下の結論を得た。 1. イオン偏析によってニオブ酸リチウム成長界面に結晶化起電力が発生する 2. コングルエント組成であってもイオン種の平衡分配係数は１では無い 3. イオン性融液からの結晶成長における分配を正確に理解するためには、イオン種の分配について考慮しなければならない
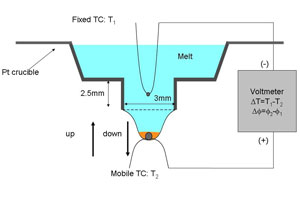図2：マイクロ引き下げ法を用いた内部電場測定系	マイクロ引き下げ法を用いた界面近傍の内部電場測定 本研究では、マイクロ引き下げ法を用いて内部電場の測定を行った。ニオブ酸トリウムの組成は、 コングルエント組成（Li2O=48.38 mol%）を用いた。図２に示すように、マイクロ引き下げ成長の 白金るつぼに、二組の熱電対（上：固定、下：上下動可）を設置し、それらの温度差と電位差を同時計測することに よって、液相·固相のゼーベック係数及び結晶化起電力を評価することができる。実験では、下側熱電対を 引き下げることによって熱電対を種結晶とする結晶成長を行い、その際の2点間の温度差と電位差を測定した。 長さ1mm程度の結晶（c軸方向の単結晶が得られる）が成長した後、成長を停止させ、今度は下側熱電対を押し上げ ながら結晶を融解し、引き下げ過程と同様に融解過程における温度差及び電位差を測定した。マイクロ引き下げ法は、 細いキャピラリーノズル中及びモルテンゾーン中における自然対流が無いために、溶質の輸送について、完全な1次元解析を 行うことが可能である。本研究では、解析においてこの特徴を駆使した。
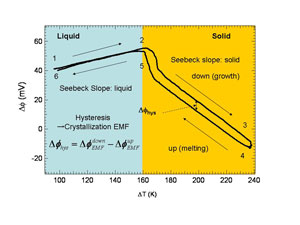図3：電位差 温度差曲線	電位差­温度差曲線 図３に、マイクロ引き下げ法を用いて測定した2つの熱電対間の温度差­電位差曲線を示す。この曲線は、 （１）液相·固相におけるゼーベック効果による電位スロープ（２）固相側ヒステリシスに現われる結晶化起電力、 によって構成されている。 ゼーベック係数の評価：液相及び固相における電位スロープの傾きから、各相のゼーベック係数を求めた： 液相： αL=0.23 mV/K、固相： αS=-0.71 mV/K 結晶化起電力：固相側ヒステリシスは、結晶成長過程（引き下げ過程）における結晶化起電力と融解過程 （押し上げ過程）における結晶化起電力の足し合わせとして電位差曲線に現われる。
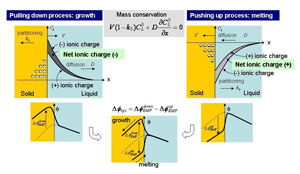図4：結晶化起電力のモデル。 左が成長過程、右が融解過程	モデル：イオン偏析による結晶化起電力発生 我々は、結晶化起電力がイオン偏析によって発生する、というモデルを提案した（図４）。融液中の正負イオン種が 1で無い、かつ、異なる平衡分配係数を持つ場合、界面近傍における正負イオン種の分布には差が生じるために、 正味のイオン電荷分布が形成される（図４中ハッチの部分）。成長過程では、この正味のイオン電荷が負の符号を持ち、 それによって固相側に正の電荷分布が形成され、その結果界面に起電力が発生する。融解プロセス（押し上げ過程） では、正負イオン種の分布関係が逆転するため、正味のイオン電荷の符号は正となり、成長時とは逆符号の起電力が 発生する。測定した温度差­電位差曲線におけるヒステリシスは、成長時と融解時のヒステリシスが足しあわされた ものとして説明することができる。
図5：電場を考慮した1次元解析	成長速度依存性の1次元解析 イオン偏析によって結晶化起電力が発生するモデル[3]を用いて、結晶化起電力の成長速度依存性の解析を行った。 融液内には複数のイオン種が存在すると考えられるが、ここでは、それらを代表する仮想的な2種類の正·負イオン種を 仮定し、1次元解析を行った[6]。解析の概要を以下に示す。 （１）仮想的な正·負イオン種の平衡分配係数、拡散定数を仮定する。 （２）電場によるドリフトを考慮したイオン種のフラックス式を立て、定常状態における1次元微分方程式を適切な 境界条件によって解き、両イオン種の融液内における濃度分布を解析的に算出する。 ＊図5に、電場を考慮したフラックス式、及び成長界面における質量保存式を示す。イオンをドリフトする電場には 、イオン自身が作り出す結晶化起電力の電場とゼーベック効果による電場がある。 ＊電場を含むフラックス式及び質量保存式は、図6に示す変数変換を行うことにより、一般的な形式を変換すること ができる[3,7]。 ＊図7に、定常状態におけるイオン濃度計算に用いた微分方程式及び境界条件を示す[6]。
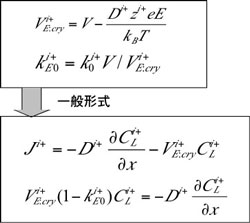図6：パラメータの変換	図7：1次元解析における微分方程式と境界条件
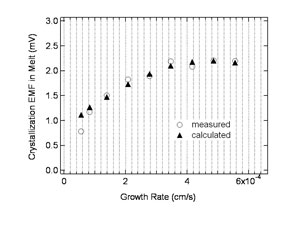図8：結晶化起電力の成長速度依存性。 ○が測定値、▲が計算値	ポアソン方程式を用いたポテンシャル計算と最適化 求めた正負イオンに関する濃度分布を用いて、両イオン種の濃度分布の差として表現される正味のイオン電荷濃度を 計算することができる。この正味のイオン電荷分布についてポアソン方程式を解き、イオン電荷によって界面融液側に 形成されるポテンシャル分布を解析的に算出することができる。この計算によって求められるポテンシャルが融液内で 発生する結晶化起電力であるとして、実験データに対してパラメータ（平衡分配係数、拡散定数、誘電率とバルク 融液中のイオン濃度の比）の最適化を行った。 以上の解析、最適化を通して、図8に示すように、結晶化起電力の成長速度依存性の実験データを再現することが できた（○が実験値、 ▲が計算値）。これは、イオン偏析によって結晶化起電力が 発生する、というモデルの妥当性を示していると考えている。 また、最適化によって、仮想的な正負イオン種の平衡分配係数及び拡散定数を K0+=0.85, D+=1.7×10-5 cm2/s K0-=0.21, D-=3.4×10-5 cm2/s と決定した。また、融液の比誘電率は∼105程度であると見積もられた。これは、融液が 高いイオン性伝導率を持ち、多くのイオンキャリアが存在することを示している。
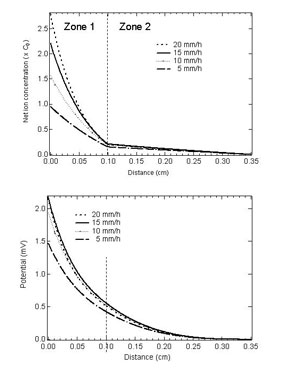図9：最適化したパラメータを用いて計算した、異なる成長速度における正味のイオン電荷分布（上）とポテンシャル分布（下）。	まとめ 本研究を通して、イオンの分配、及びそれに起因する結晶化起電力についての知見を得ることができた。これは、 イオン性融液からの結晶成長における普遍的な知見であり、結晶成長への新たな視点を提示したものである。 参考文献 [1] S. Uda and W. A. Tiller, J. Crystal Growth 121 (1992) 155. [2] W. A. Tiller, S. Uda, J. Crystal Growth 129 (1993) 341. [3] S. Uda and W.A. Tiller, J. Crystal Growth 121 (1992) 93. [4] V.A. D'yakov et al., Bull. Acad. Sci. USSR, Phys. Ser. 49 (1985) 117. [5] S. Koh, S. Uda, M. Nishida, X. Huang, J. Cryst. Growth 297 (2006) 247. [6] S. Uda et al., J. Crystal Growth 167 (1996) 64. [7] W.A. Tiller and R. F. Sekerka, J. Appl.Phys. 35 (1964) 2726.